AndrewNG-Deep Learning 基础

1 Logistic Regression Model

1.1 Binary Classification

To learn a classifier that can input an image represented by the feature vector x, and predict the corresponding label y.

Notation——n training examples: ($ n_x $为向量维数，$X$为$ n_x\times m $矩阵) $$ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}), …, (x^{(m)},y^{(m)}),x\in R^{n_x}, y\in {0,1} $$

$$ X=[x^{(1)},x^{(2)},…,x^{(m)}], X\in R^{n\times m} $$

$$ Y=[y^{(1)},y^{(2)},…,y^{(m)}], Y\in R^{1\times m} $$

1.2 Logistic Regression

An algorithm for binary classification problems.

Given x, we want $\hat{y}=P(y=1|x)$​

Way:

  • Parameters: $w\in R^{nx},b\in R$

  • Output: （$\sigma$为sigmoid函数，$\sigma(z)=\frac{1}{1+e^{-z}}$）

    $$ \hat{y}=\sigma(w^Tx+b), (z = w^Tx+b) $$

1.3 Cost Function

we want $\hat{y(i)}\approx y(i)$

Loss(error) function: $L(\hat{y},y)=-(y·log\hat{y}+(1-y)log(1-\hat{y}))$​

  • $\hat{y(i)}$与$y(i)$越接近，$L(\hat{y},y)$越小
  • If $y=1$: $L(\hat{y},y)=-log\hat{y}$
  • If $y=0$: $L(\hat{y},y)=-log(1-\hat{y})$

It measures how well you’re doing on a single training example.

Cost function:$J(w,b)=\frac{1}{m}\sum_{i = 1}^{m}L(\hat{y}^{(i)},y^{(i)})$

It measures how well you’re doing on the entire training set.

1.4 Gradient Descent

An algorithm to learn the parameteres w and b on your training set.

$$ w := w-\alpha\frac{\partial J(w,b)}{\partial w}, b:=b-\alpha\frac{\partial J(w,b)}{\partial b} $$

$\alpha$​​​​ is the learning rate.

Derivatives (导数)

Computation Graph

backward propagation

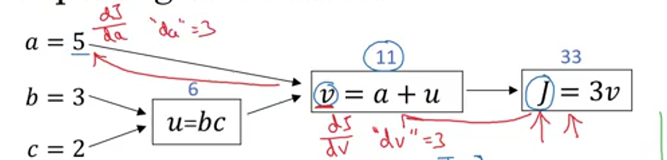
image-20210806212057599

在代码中，可以用dv，da作为变量名。

$$ \frac{dJ}{dc}=\frac{dJ}{dv}\frac{dv}{du}\frac{du}{dc}=3\times1\times3=9 $$

Gradient Descent on 1 example

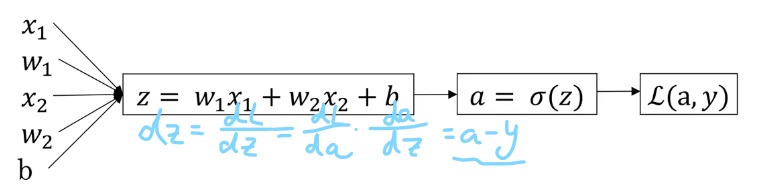image-20210806213958503 $$ w_1 := w_1-\alpha\frac{\partial dL}{\partial w},w_2 := w_2-\alpha\frac{\partial dL}{\partial w2},b := b-\alpha\frac{\partial dL}{\partial b} $$

Gradient Descent on m examples

Neural network programming guideline: Whenever possible, avoid explicit for-loops.

Use vectorization.

Forward Propagation: $$ A=\sigma\left(w^{T} X+b\right)=\left(a^{(1)}, a^{(2)}, \ldots, a^{(m-1)}, a^{(m)}\right) $$

  • Cost function:

$$ J=-\frac{1}{m} \sum_{i=1}^{m}\left(y^{(i)} \log \left(a^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-a^{(i)}\right)\right) $$

Backward Propagation:

$$ \frac{\partial J}{\partial w}=\frac{1}{m} X(A-Y)^{T} $$

$$ \frac{\partial J}{\partial b}=\frac{1}{m} \sum_{i=1}^{m}\left(a^{(i)}-y^{(i)}\right) $$

Code of Optimizing procedure:

def propagate(w, b, X, Y):
    m = X.shape[1]
    
    # Forward propogation
    A = sigmoid(np.dot(w.T, X)+b);
    cost = -np.average(Y*np.log(A)+(1-Y)*np.log(1-A))
    
    #Backward propagation
    dw = np.dot(X, (A-Y).T)/m
    db = np.average(A-Y)

    cost = np.squeeze(np.array(cost))
    grads = {"dw": dw,
             "db": db}
    return grads, cost


def optimize(w, b, X, Y, num_iterations=100, learning_rate=0.009, print_cost=False):
    for i in range(num_iterations):
            grads, cost = propagate(w, b, X, Y)
            dw = grads["dw"]
            db = grads["db"]
            w = w - learning_rate*dw;
            b = b - learning_rate*db;

1.5 Python Skill

Broadcasting

A = np.array([1,2,3,4],
			[5,6,7,8],
			[9,10,11,12])
cal = A.sum(axis=0) # axis=0垂直方向求和,axis=1水平方向求和
percentage=A/cal.reshape(1,4) # broadcasting(1,4)->(3,4))

不要用rank=1(秩为1)的array,而要用5*1的矩阵

a = np.random.randn(5) # bad
a = np.random.randn(5,1) # good
assert(a.shape==(5,1))

2 One hidden layer Neural Network

2.1 Neural Network Representation

One hidden layer NN also called a two layer NN (不算输入层)

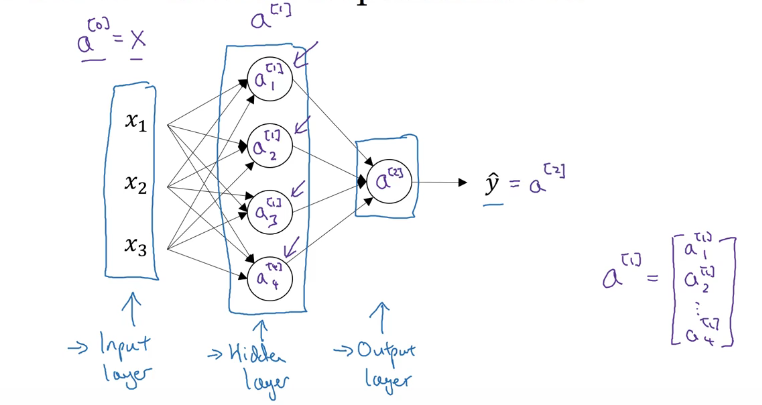
image-20210807193618855

2.2 Forward Propagation

On single training example:

$$ z^{[1]}=W^{[1]} x+b^{[1]}, a^{[1]}=\sigma(z^{[1]}) $$

$$ z^{[2]}=W^{[2]} a^{[1]}+b^{[2]}, a^{[2]}=\sigma(z^{[2]}) $$

vectorizing across multiple examples:

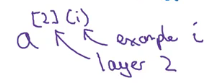image-20210808114345333 $$ Z^{[1]} =W^{[1]} X+b^{[1]},A^{[1]}=g^{[1]}(Z^{[1]}), $$

$$ Z^{[2]} =W^{[2]} A^{[1]}+b^{[2]},A^{[2]}=g^{[2]}(Z^{[2]})=\sigma(Z^{[2]}) $$

2.3 Activation functions

  • tanh: $a=\frac{e^z-e^{-z}}{e^z+e^{-z}}$

tanh函数在绝大多数场景下比$\sigma$​函数更适合用作激活函数；唯独在binary classification的输出层，$\sigma$​​函数更适合用作激活函数。

  • Relu: a=max(0, z)

Relu函数可解决梯度消失的问题，优于tanh函数和$\sigma$​函数。除了输出层，默认作为激活函数。

  • Leaky Relu: a = max(0.01z, z)

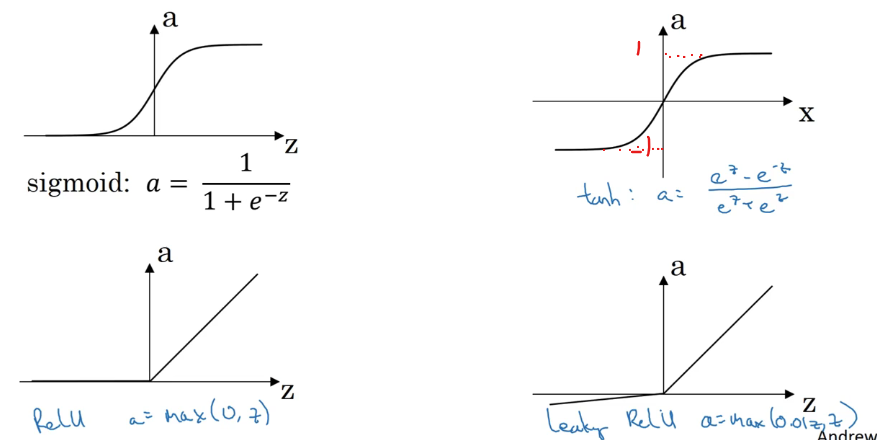
image-20210808114900557

2.4 Derivatives of Activation functions

  • g(z)=$\sigma$​(z): $g'(z)=a(1-a)$
  • g(z)=tanh(z): $g'(z)=1-a^2$​
  • ReLU:

$$ g'(z)=\left\{ \begin{aligned} 0 & & z<0 \\ 1 & & z\geq0 \end{aligned} \right. $$

  • Leaky ReLU:

$$ g'(z)=\left\{ \begin{aligned} 0.01 & & z<0 \\ 1 & & z\geq0 \end{aligned} \right. $$

2.5 Gradient descent for neural networks

backward propagation:

$$ dZ^{[2]}=A^{[2]}-Y $$

$$ dW^{[2]}=\frac{1}{m}dZ^{[2]}A^{[1]T} $$

$$ db^{[2]}=\frac{1}{m}np.sum(dZ^{[2]},axis=1,keepdim=True) $$

$$ d Z^{[1]}=W^{[2] T} d Z^{[2]} * g^{[1]^{\prime}}\left(\mathrm{Z}^{[1]}\right) $$

$$ d W^{[1]}=\frac{1}{m} d Z^{[1]} X^{T} $$

$$ d b^{[1]}=\frac{1}{m} np.sum(d Z^{[1]}, axis=1, keepdims=True) $$

  • keepdim=True: 用于防止输出$(n^{[2]},)$，而是输出$(n^{[2]},1)$

2.6 Random Initialization

在Neural network中，w不能初始化为全0。

$$ w^{[1]}=np.random.randn((2,2))*0.01 $$

$$ b^{[2]}=np.zero((2,1)) $$

$$ w^{[1]}=np.random.randn((1,2))*0.01 $$

$$ b^{[2]}=0 $$

3 Deep Neural Network

  • layers: L = 4
  • ouput: $\hat{y}=a^{[L]}$

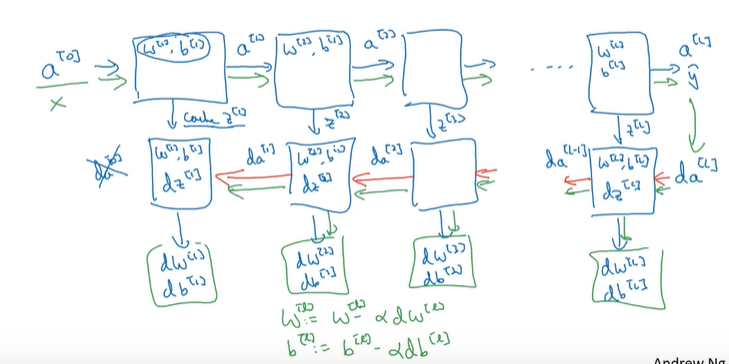
3.1 Forward Propagation

for l=1…4: $$ Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]} $$

$$ A^{[Ll}=g^{[l]}(Z^{[l]}) $$

3.2 Backward Propagation

  • Input $da^{[l]}$​
  • Output $da^{[l-1},dW^{[l]},db^{[l]}$

$$ dZ^{[l]}=dA^{[l]}*{g^{[l]}}'(Z^{[l]}) $$

$$ dW^{[l]}=\frac{1}{m}dZ^{[l]}·A^{[l-1]T} $$

$$ db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]},AXIS=1, keepdims=True) $$

$$ dA^{[l-1]}=W^{[l]T}dZ^{[l]} $$

3.3 Matrix dimensions

  • $W^{[l]},dW^{[l]}:(n^{[l]},n^{[l-1]})$
  • $b^{[l]},db^{[l]}:(n^{[l]},1)$
  • $z^{[l]},a^{[l]}:(n^{[l]},1)$
  • $Z^{[l]},A^{[l]},dZ^{[l]},dA^{[l]}:(n^{[l]},m)$

3.4 Working procedure

image-20210810111918024

3.5 Parameters & Hyperparameters

Hyperparameters control the parameters.

Paramerters:

  • $W^{[a]},b^{[a]}$​

Hyperparematers:

  • learning rate $\alpha$​
  • iterations
  • hidden layers L
  • ……