排序方法总结

排序方法时间复杂度（平均）时间复杂度（最好）时间复杂度（最坏）空间复杂度稳定性
冒泡排序O(n^2)O(n)O(n^2)O(1)稳定
插入排序O(n^2)O(n)O(n^2)O(1)稳定
快速排序O(nlogn)O(nlogn)O(n^2)O(nlogn)不稳定
归并排序O(nlogn)O(nlogn)O(nlogn)O(n^2)稳定
堆排序O(nlogn)O(nlogn)O(nlogn)O(1)不稳定

冒泡排序

依次比较相邻元素，并把大数向后交换，比完一轮后最大的数换到了最后。

重复以上步骤，将第二大的元素放到倒数第二位…

插入排序

对于未排序元素，在已排序序列中从后向前扫描，找到相应位置并插入。

void merger_sort(Type A[], int left, int right) {
    if(left < right) {
        int middle = (left+right)/2;
        merger_sort(A, left, middle);
        merger_sort(A, middle, right);
        merge(A, B, left, middle, right);//合并到数组B
        copy(A, B, left, right);//复制回数组A
    }
}

void merge(Type A[], Type B, int left, int middle, int right)
{
    int i = left, j = middle+1, k=1;
    while((i < middle) && (j <= right)) {
        if(c[i] <= c[j])
            d[k++] = c[i++];
        else
            d[k++] = c[j++];
    }
    if(i > middle) {
        for(int q = j; q < m; q++)
            d[k++] = c[q];
    }
    else {
        for(int q = i; q <= m; q++)
            d[k++] = c[q];
    }
}

快速排序

从数列中挑一个元素，作为“基准”(pivot)。

将比基准小的元素放在基准前面，比基准大的元素放在基准后面。

递归地对两个子序列进行快排。

int partition(int num[], int left, int right) {
    int x = num[right];
    int i = left;
    int j = left - 1;
    for (; i < right; i++) {
        if (num[i] < x) {
            j++;
            if (j != i)
                swap(num[j], num[i]);
        }
    }
    swap(num[j + 1], num[right]);
    return j + 1;  //返回分割点
}

void quick_sort(int num[], int left, int right) {
    if (left < right) {
        int index = partition(num, left, right);
        quick_sort(num, left, index - 1);
        quick_sort(num, index + 1, right);
    }
}

快速排序的稳定版（Java，使用额外空间）：

public int[] quickSort(int[] num) {
    ArrayList<Integer> ar = new ArrayList<>();
    for (int i : num) ar.add(i);
    ArrayList<Integer> ans = quickSort(ar);
    for (int i = 0; i < num.length; i++)
        num[i] = ans.get(i);
    return num;
}
public static ArrayList<Integer> quickSort(ArrayList<Integer> ar) {
    if(ar.size() <= 1) return ar;

    int mid = ar.size() / 2;
    int pivat = ar.get(mid);

    ArrayList<Integer> smaller = new ArrayList<>();
    ArrayList<Integer> greater = new ArrayList<>();
    for(int ind = 0; ind < ar.size(); ind++) {
        int val = ar.get(ind);
        if( ind != mid ) {
            if( val < pivat ) smaller.add(val);
            else if(val > pivat) greater.add(val);
            else {                   
                if(ind < mid) smaller.add(val);
                else greater.add(val);
            }
        }
    }
    ArrayList<Integer> ans = new ArrayList<Integer>();              
    ArrayList<Integer> sa1 = quickSort(smaller);
    ArrayList<Integer> sa2 = quickSort(greater);

    for(Integer val1 : sa1)  ans.add(val1);  
    ans.add(pivat);
    for(Integer val2 : sa2)  ans.add(val2);

    return ans;        
    }

归并排序

分治法。将两个已经排序的序列合并。

void merge_sort(int num[], int first, int end) {
    if (first < end) {
        int mid = (first + end) / 2;
        merge_sort(num, first, mid);
        merge_sort(num, mid + 1, end);
        merge(num, first, mid, end);
    }
}

void merge(int num[], int first, int mid, int end) {
    int n1 = mid - first + 1;
    int n2 = end - mid;
    int* L = new int[n1];
    int* R = new int[n2];
    for(int i = 0; i < n1; i++)
        L[i] = num[first + i];

    for (int j = 0; j < n2; j++)
        R[j] = num[mid + j + 1];

    int i = 0;
    int j = 0;
    int k = first;
    while(i < n1 && j < n2) {
        if (L[i] < R[j])
            num[k++] = L[i++];
        else
            num[k++] = R[j++];
    }

    while (i < n1) num[k++] = L[i++];
    while (j < n2) num[k++] = R[j++];
    
    delete [] L;
    delete [] R;
}

堆排序

堆本质上是一个数组，且我们以二叉树的角度来看待他。

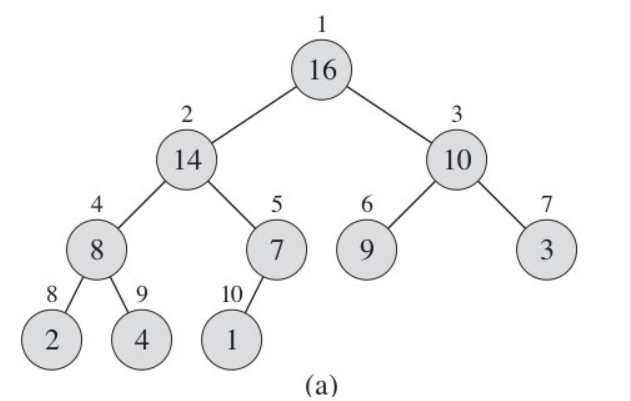
image-20210827161426717

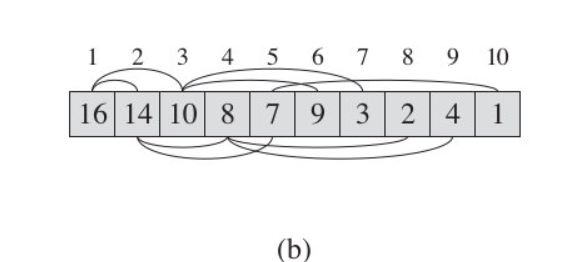
image-20210827161442509

实际数组下标以0开始，故：

  • 左子结点的编号=父结点编号 * 2 +1
  • 右子结点的编号=父结点编号 * 2 + 2

堆排序的步骤（以从小到大为例）：

  1. 建立最大堆：建立一颗满足如下条件的二叉树：它的所有的结点的值都比其子结点的值大。建立过程如下：
    • 从后往前，从第一个非叶节点开始，进行调整（比较该节点是否大于其子节点，若不满足则向下交换）。
  2. 每次取走根节点的元素（最大元素），用数组末尾的元素代替，然后进行调整
//检查以root为根的子树是否满足大根堆性质，若不满足，则向下调整
void heap_build(int num[], int root, int len) { 
    int lchild = root * 2 + 1;
    if (lchild < len) {
        int largest = lchild;
        int rchild = lchild + 1;
        if (rchild < len) {
            if (num[rchild] > num[largest])
                largest = rchild;
        }
        if (num[root] < num[largest]) {
            swap(num[root], num[largest]);
            heap_build(num, largest, len);
        }
    }
}

void heap_sort(int num[], int len) {
    for (int i = len / 2-1; i >= 0; i--) // 从第一个非叶节点，从后往前调整
        heap_build(num, i, len);

    for (int j = len - 1; j >= 1; j--) { // 不断取根节点，并将剩下元素重新构建大根堆
        swap(num[0], num[j]);
        heap_build(num, 0, --len);
    }
}

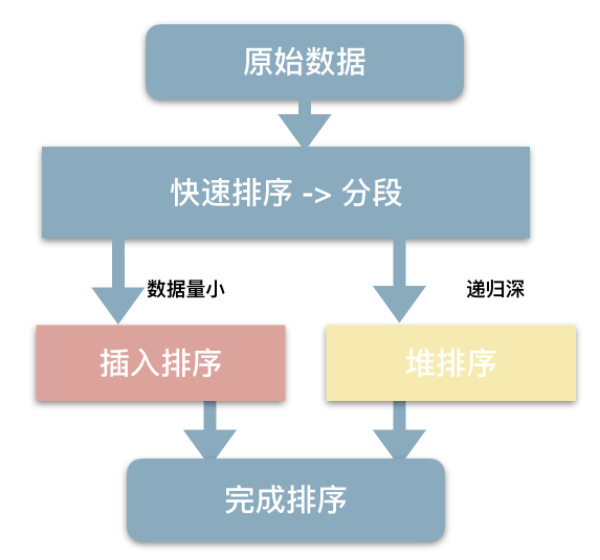
C++ STL中sort的底层实现

数据量大时采用QuickSort快排算法。一旦分段后的数据量小于某个门槛（16），为避免QuickSort快排的递归调用带来过大的额外负荷，就改用Insertion Sort插入排序。如果递归层次过深，还会改用HeapSort堆排序。

image-20210925113042086